问题
解答题
设函数f（x）=x2-2|x|-1（-3≤x≤3）
（1）证明f（x）是偶函数；
（2）指出函数f（x）的单调增区间；
（3）求函数的值域．
答案
（1）由于函数f（x）=x2-2|x|-1（-3≤x≤3）的定义域关于原点对称，
且满足f（-x）=（-x）2-2|-x|-1=x2-2|x|-1=f（x），
故函数f（x）为偶函数．
（2）由于函数f（x）=
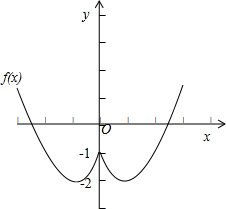
，如图所示：x2-2x-1，x≥0 x2+2x-1，x＜0
故它的单调增区间为[-1，0]、[1，+∞）．
（3）结合函数的图象可得函数没有最大值，当x=±1 时，函数取得最小值为-2，
故函数的值域为[-2，+∞）．
