问题
解答题
已知双曲线的焦点在y轴上，两顶点间的距离为4，渐近线方程为y=±2x，
（Ⅰ）求双曲线的标准方程；
（Ⅱ）设（Ⅰ）中双曲线的焦点F1，F2关于直线y=x的对称点分别为F1′，F2′，求以F1′，F2′为焦点，且过点P（0，2）的椭圆方程。
答案
解：（Ⅰ）因为双曲线的焦点在y轴上，
设所求双曲线的方程为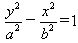
，
由题意，得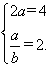
，解得a=2，b=1，
所求双曲线的方程为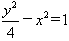
；
（Ⅱ）由（Ⅰ）可求得F1（0，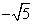
），F2（0，
），
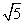点F1，F2关于直线y=x的对称点分别为F1′（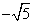
，0），F2′（
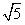，0），
又P（0，2），设椭圆方程为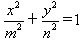
（m＞n＞0），
由椭圆定义，得2m=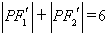
，m=3，
因为m2-n2=5，
所以n2=4，
所以椭圆的方程为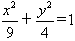
。