问题
选择题
定义在R上的偶函数f(x),满足f(x+
|
答案
∵f(x)是偶函数,
∴f(-x)=f(x)
∵f(x+
)=-f(x+1 2
),3 2
∴f(x)=-f(x+1)
∴f(x)=f(2-x)
∴函数的图象关于x=1对称
∵在区间[-1,0]上为递增,
∴在区间[0,1]上为递减,
我们可以作出一个函数图象:
易得:f(3)<f(
)<f(2)2
故选A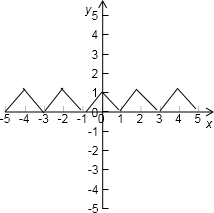
定义在R上的偶函数f(x),满足f(x+
|
∵f(x)是偶函数,
∴f(-x)=f(x)
∵f(x+
)=-f(x+1 2
),3 2
∴f(x)=-f(x+1)
∴f(x)=f(2-x)
∴函数的图象关于x=1对称
∵在区间[-1,0]上为递增,
∴在区间[0,1]上为递减,
我们可以作出一个函数图象:
易得:f(3)<f(
)<f(2)2
故选A