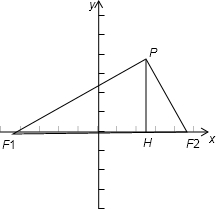
在平面直角坐标系xOy中，已知两点F₁（-6，0）、F₂（6，0），

且tan∠PF1F2=

2

11

，tan∠PF₂F₁=2．

∴P（5，2），如图．

（1）由题意可设所求椭圆的标准方程为

x2

a2

+

y2

b2

=1（a＞b＞0），

其半焦距c=6

2a=|PF1|+|PF2|=

112+22

+

12+22

=6

5

∴a=3

5

，b²=a²-c²=9．

所以所求椭圆的标准方程为

x2

45

+

y2

9

=1

（2）点P（5，2）、F₁（-6，0）、F₂（6，0）

设所求双曲线的标准方程为

x2

a 21

-

y2

b 21

=1(a1＞0，b1＞0)

由题意知，半焦距

c₁=6 2a1=||P′F1′|+|P′F2′||=|

112+22

-

12+22

|=4

5

a1=2

5

，

b₁²=c₁²-a₁²=36-20=16．

所以所求双曲线的标准方程为

x2

20

-

y2

16

=1