问题
解答题
(1)焦点在y轴上的椭圆的一个顶点为A(2,0),其长轴长是短轴长的2倍,求椭圆的标准方程.
(2)已知双曲线的一条渐近线方程是x+2y=0,并经过点(2,2),求此双曲线的标准方程.
答案
解:(1)由题可知b=2,a=4,椭圆的标准方程为:
(2)设双曲线方程为:x2﹣4y2=λ,
∵双曲线经过点(2,2),
∴λ=22﹣4×22=﹣12,
故双曲线方程为: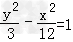 .
.
(1)焦点在y轴上的椭圆的一个顶点为A(2,0),其长轴长是短轴长的2倍,求椭圆的标准方程.
(2)已知双曲线的一条渐近线方程是x+2y=0,并经过点(2,2),求此双曲线的标准方程.
解:(1)由题可知b=2,a=4,椭圆的标准方程为:
(2)设双曲线方程为:x2﹣4y2=λ,
∵双曲线经过点(2,2),
∴λ=22﹣4×22=﹣12,
故双曲线方程为: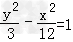 .
.