问题
解答题
已知中心在坐标原点O的椭圆C经过点A(2，3)，且点F(2，0)为其右焦点，
(Ⅰ)求椭圆C的方程；
(Ⅱ)是否存在平行于OA的直线l，使得直线l与椭圆C有公共点，且直线OA与l的距离等于4？若存在，求出直线l的方程；若不存在，说明理由．
答案
解：(Ⅰ)依题意，可设椭圆C的方程为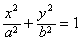
(a＞b＞0），
且可知左焦点为F′(-2，0)，从而有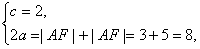
，
解得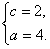
，
又a2=b2+c2，所以b2=12，
故椭圆C的方程为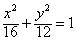
。
(Ⅱ)假设存在符合题意的直线l，其方程为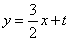
，
由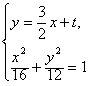
得3x2+3tx+t2-12=0，
因为直线l与椭圆C有公共点，所以△=(3t)2-4×3(t2-12)≥0，
解得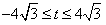
。
另一方面，由直线OA与l的距离d=4可得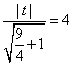
，
从而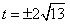
，
由于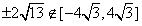
，
所以符合题意的直线l不存在。