问题
解答题
在直角坐标系xOy上取两个定点A1(-2,0),A2(2,0),再取两个动点N1(0,m),N2(0,n),且mn=3。
(1)求直线A1N1与A2N2交点的轨迹M的方程;
(2)已知点G(1,0)和G′(-1,0),点P在轨迹M上运动,现以P为圆心,PG为半径作圆P,试探究是否存在一个以点G′(-1,0)为圆心的定圆,总与圆P内切?若存在,求出该定圆的方程;若不存在,请说明理由.
答案
解:(1)依题意知,直线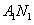 的方程为:
的方程为: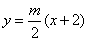 ,①
,①
直线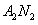 的方程为:
的方程为: , ②
, ②
设Q(x,y)是直线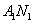 与
与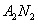 的交点,①×②得
的交点,①×②得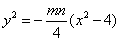 ,
,
由mn=3,整理得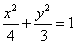 ,
,
∵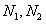 不与原点重合,
不与原点重合,
∴点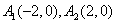 不在轨迹M上,
不在轨迹M上,
∴轨迹M的方程为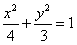 (x≠±2)。
(x≠±2)。
(2)由(1)知,点G(1,0)和G′(-1,0)为椭圆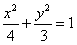 的两焦点,
的两焦点,
由椭圆的定义,得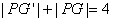 ,即
,即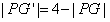 ,
,
∴以G′为圆心,以4为半径的圆与⊙P内切,
即存在定圆⊙G′,该定圆与⊙P恒内切,其方程为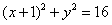 。
。
