问题
解答题
已知椭圆C的两个焦点分别为F1（-1，0），F2（1，0），点在椭圆C上，抛物线E以椭圆C的中心为顶点，F2为焦点。
（1）求椭圆C的方程；
（2）直线l过点F2，且交y轴于D点，交抛物线E于A，B两点，
①若F1B⊥F2B，求|AF2|-|BF2|的值；
②试探究：线段AB与F2D的长度能否相等？如果|AB|=|F2D|，求直线l的方程。
答案
解：（1）由题意，设椭圆C的方程为：
∴
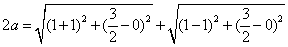=4
∴a=2
又c=1
∴
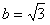
故椭圆C的方程为：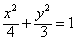
。
（2）由题意可得，抛物线E：y2=4x，
设l：y=k（x-1）（k≠0），
联立方程组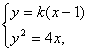
消去y得：k2x2-2（k2+2）x+k2=0，
Δ=16（k2+1）>0恒成立
设A（x1，y1），B（x2，y2），
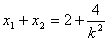，x1·x2=1
①∵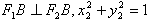
又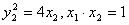
，
∴
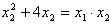
∴x1-x2=4，
|AF2|-|BF2|=x1-x2=4。
②假设|AB|=|F2D|
因为直线l过点F2，
所以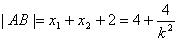
又D（0，-k），F2（1，0）
∴
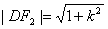
由|AB|=|F2D|
∴
∴k4-16k2-16=0，
所以
（负值舍去），
从而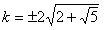
，
所以当l的方程为
时有|AB|=|F2D|。