问题
解答题
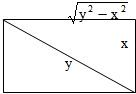
(1)一个矩形的面积为8,如果此矩形的对角线长为y,一边长为x,试把y表示成x的函数.
(2)证明:函数f(x)=x2+1是偶函数,且在[0,+∞)上是增函数.
答案
(1)如图,x
=8y2-x2
则:y2=x2+8 x2
y=
(x>0)x2+ 8 x2
(2)证明:∵f(-x)=(-x)2+1=x2+1=f(x),∴函数f(x)=x2+1是偶函数,
作取x1,x2∈[0,+∞),令x1<x2
f(x1)-f(x2)=x12-x22=(x1-x2)(x1+x2)
∵x1,x2∈[0,+∞),令x1<x2
∴x1-x20
∴f(x1)-f(x2)=x12-x22=(x1-x2)(x1+x2)<0
故函数在[0,+∞)上是增函数.
综上,函数f(x)=x2+1是偶函数,且在[0,+∞)上是增函数.