（本小题满分14分）已知数列{an}的前n项和为Sn，且an是Sn与2的等

问题解答题

（本小题满分14分）已知数列{a_n}的前n项和为S_n，且a_n是S_n与2的等差中项，数列{b_n}中，b₁=1，点P（b_n，b_n+₁）在直线x-y+2=0上。

（1）求a₁和a₂的值；（2）求数列{a_n}，{b_n}的通项a_n和b_n；

答案

解：（1）∵a_n是S_n与2的等差中项 ∴S_n=2a_n-2 ∴a₁=S₁=2a₁-2，解得a₁=2

a₁+a₂=S₂=2a₂-2，解得a₂="4"

（2）∵S_n=2a_n-2，S_n_-1=2a_n_-1-2，又S_n—S_n_-1=a_n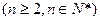， ∴a_n=2a_n-2a_n_-1， ∵a_n≠0，

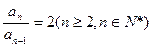∴，即数列{a_n}是等比数列 ∵a₁=2，∴a_n=2ⁿ

∵点P(b_n，b_n₊₁)在直线x-y+2=0上，∴b_n-b_n₊₁+2=0，

∴b_n₊₁-b_n=2，即数列{b_n}是等差数列，又b₁=1，∴b_n=2n-1