问题
选择题
设等差数列{an}的前n项和为Sn，若a1＝－11，a4＋a6＝－6，则当Sn取最小值时，n等于( )
A．6
B．7
C．8
D．9
答案
答案：A
分析：条件已提供了首项，故用“a1，d”法，再转化为关于n的二次函数解得．
解答：解：设该数列的公差为d，则a4+a6=2a1+8d=2×（-11）+8d=-6，解得d=2，
所以Sn=-11n+
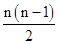×2=n2-12n=(n-6)2-36，所以当n=6时，Sn取最小值．
故选A
点评：本题考查等差数列的通项公式以及前n项和公式的应用，考查二次函数最值的求法及计算能力．