问题
选择题
若(m+1)x2-(m-1)x+3(m-1)<0对任意实数x恒成立,则实数m的取值范围是( )
|
答案
∵(m+1)x2-(m-1)x+3(m-1)<0对任意实数x恒成立,
①当m+1=0,即m=-1时,不等式为x<0,不符合题意;
②当m+1≠0,即m≠-1时,由(m+1)x2-(m-1)x+3(m-1)<0对任意实数x恒成立,
∴
,解得m<-‘m+1<0 (m-1)2-12(m+1)(m-1)<0
,13 11
∴实数m的取值范围是m<-‘
.13 11
故选C.

 ,在弹簧末端处的纸板上刻上水平线A;再将质量为100g的垫圈用胶带固定于弹簧的下端,在垫圈静止时的弹簧末端处刻上水平线B;然后在B的下方刻一水平线C,使AB间距离等于BC间距,假定当地重力加速度值g=10m/x2。当加速度器在竖直方向运动,垫圈相对纸板静止时 ( )
,在弹簧末端处的纸板上刻上水平线A;再将质量为100g的垫圈用胶带固定于弹簧的下端,在垫圈静止时的弹簧末端处刻上水平线B;然后在B的下方刻一水平线C,使AB间距离等于BC间距,假定当地重力加速度值g=10m/x2。当加速度器在竖直方向运动,垫圈相对纸板静止时 ( )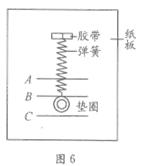
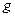 ,且方向向上
,且方向向上