问题
选择题
等差数列{an}共有2n+1项，其中奇数项之和为4，偶数项之和为3，则n的值是
A．3
B．5
C．7
D．9
答案
答案：A
题目分析：利用等差数列的求和公式和性质得出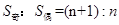
，来解得。解：设数列公差为d，首项为a1，奇数项共n+1项，其和为S奇=（n+1）an+1=4，偶数项共n项，其和为S偶=nan+1=3，由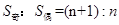，可知n的值为3，选A.
点评:本题考查等差数列的求和公式和性质，熟练记忆并灵活运用求和公式是解题的关键，属基础题