问题
解答题
(13分) 已知等比数列{an}中，a2＝2，a5＝128．
(1) 求通项an；
(2) 若bn = log2an，数列{bn}的前n项和为Sn，且Sn = 360，求n的值．
答案
(1) an＝a2·qn—2＝2·4n—2＝22n—3 ；(2) n＝20为所求
本试题主要是考查了数列的概念和数列求和的综合运用。
（1）根据等比数列{an}中，首项和公比来表示已知中a2＝2，a5＝128．，，得到通项公式。
（2）结合上一问的结论，
bn＝log222n－3＝2n－3，然后利用等差数列求和得到结论。
解：(1) 设公比为q，由a2＝2，a5＝128及a5＝a2q3得 128＝2q3，
∴q＝4 ∴an＝a2·qn—2＝2·4n—2＝22n—3 ····················· 6分
(2) bn＝log222n－3＝2n－3 ·························· 8分
∴数列{bn}是以－1为首项，2为公差的等差数列
∴Sn＝n (－1)＋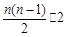
＝n2－2n ····················· 11分
令n2－2n＝360得n1＝20，n2＝－18（舍）
故n＝20为所求 ······························ 13分