在数列{an}(n∈N*)中,已知a1=1,a2k=-ak,a2k-1=(-1)k+1ak,k∈N*. 记数列{an}的前n项和为Sn.
(1)求S5,S7的值;
(2)求证:对任意n∈N*,Sn≥0.
(1) S5=3,S7=1.
(2)根据已知的递推关系,然后结合整体的思想来分析得到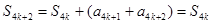 ,然后运用数学归纳法加以证明。
,然后运用数学归纳法加以证明。
题目分析:解:(1)根据题意, 由于a1=1,a2k=-ak,a2k-1=(-1)k+1ak,
故有 故可知S5=3,S7=1. 2分
故可知S5=3,S7=1. 2分
(2)由题设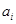 的定义可知,对于每个正整数k,有
的定义可知,对于每个正整数k,有
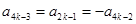 . ①
. ①
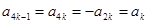 . ② 4分
. ② 4分
则 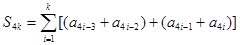
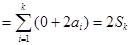 ,③
,③
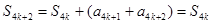 . ④ 6分
. ④ 6分
下面证明对于所有的n≥1,Sn≥0.
对于k,用数学归纳法予以证明.
当i=1,2,3,4,即k=0时,S1=1,S2=0, S3=1, S4=2.
假设对于所有的i≤4k,Si≥0,则由①、②、③、④知,
S4k+4=2Sk+1≥0,
S4k+2=S4k≥0,
S4k+3=S4k+2+a4k+3=S4k+2+a4k+4=S4k+2+(S4k+4-S4k+3),S4k+3=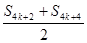 ≥0.
≥0.
接下来证明:S4k+1≥0.
若k是奇数,则S4k=2Sk≥2.
因为k是奇数,所以由题设知数列的各项均为奇数,可知Sk也是一个奇数. 于是
S4k≥2. 因此,S4k+1=S4k+a4k+1≥1.
若k是偶数,则a4k+1=a2k+1=ak+1. 所以S4k+1=S4k+a4k+1=2Sk+ak+1=Sk+Sk+1≥0.
综上,对于所有的n≥1,Sn≥0. 10分
点评:解题的关键是通过具体的例子归纳猜想结论,结合数学归纳法加以证明,属于中档题。
