问题
解答题
已知{an}为等差数列，且a1＋a3＝8，a2＋a4＝12.
（1）{an}的通项公式；
（2）记{an}的前n项和为Sn，若a1，ak，Sk＋2成等比数列，求正整数k的值．
答案
(1) an＝2n.(2) k＝6.
题目分析：（1）利用等差数列的通项公式，借助于条件a1+a3=12，a2+a4=6，可求a1，d的值，从而可求 数列的通项公式an及它的前n项和Sn．
（2）由(1)可得Sn＝n(n＋1)，那么结合因为a1，ak，Sk＋2成等比数列得到k的值。
解：(1)设数列{an}的公差为d，由题意知
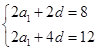解得a1＝2，d＝2.
所以an＝a1＋(n－1)d＝2＋2(n－1)＝2n.
(2)由(1)可得Sn＝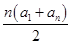
＝
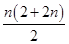＝n(n＋1)．
因为a1，ak，Sk＋2成等比数列，所以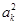
＝a1Sk＋2.
从而(2k)2＝2(k＋2)(k＋3)，即k2－5k－6＝0，
解得k＝6或k＝－1(舍去)．因此k＝6.
点评：解决该试题的关键是对于等差数列的等差中项的性质的灵活运用求解通项公式。