（1）-1       （2）4

解：(1)由f(x＋2)＝－f(x)得，

f(x＋4)＝f[(x＋2)＋2]＝－f(x＋2)＝f(x)，

所以f(x)是以4为周期的周期函数，

所以f(3)＝f(3－4)＝－f(1)＝－1.

(2)由f(x)是奇函数与f(x＋2)＝－f(x)，得f[(x－1)＋2]＝－f(x－1)＝f[－(x－1)]，即f(1＋x)＝f(1－x)．

故知函数y＝f(x)的图像关于直线x＝1对称．

又0≤x≤1时，f(x)＝x，且f(x)的图像关于原点成中心对称，则－1≤x≤0时，f(x)＝x，则f(x)的图像如图所示．

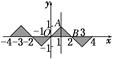
当－4≤x≤4时，设f(x)的图像与x轴围成的图形面积为S，

则S＝4S_△OAB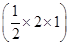＝4×＝4.