问题
填空题
若实数a,b满足a2+a-1=0,b2+b-1=0,则
|
答案
若a≠b,
∵实数a,b满足a2+a-1=0,b2+b-1=0,
∴a、b看作方程x2+x-1=0的两个根,
∴a+b=-1,ab=-1,
则
+a b
=b a
=a2+b2 ab
=a2+b2+2ab-2ab ab
=-3.(a+b)2-2ab ab
若a=b,则原式=2.
故答案为:2或-3
若实数a,b满足a2+a-1=0,b2+b-1=0,则
|
若a≠b,
∵实数a,b满足a2+a-1=0,b2+b-1=0,
∴a、b看作方程x2+x-1=0的两个根,
∴a+b=-1,ab=-1,
则
+a b
=b a
=a2+b2 ab
=a2+b2+2ab-2ab ab
=-3.(a+b)2-2ab ab
若a=b,则原式=2.
故答案为:2或-3
下表关于化学反应方程式的评价正确的是 [ ]
反应方程式 4-溴丁酸与足量的氢氧化钠溶液反应: | 评价 | |
| A | 在亚硫酸钠溶液中滴几滴新制氯水: | |
| SO32-+Cl2+H2O=SO42-+2Cl- +2H+ | 正确 | |
| B | 沸水中滴加氯化铁饱和溶液制氢氧化铁胶体: | |
Fe3+ +3H2O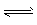 Fe(OH)3(胶体)+3H+ Fe(OH)3(胶体)+3H+ | 错误。不应该用可逆号,应 用等号,且标明加热条件 | |
| C | 0.1 mol/L H2A溶液的pH =1,H2A的电离方程式: | |
H2A=H+ +HA- ,HA-  H+ +A2- H+ +A2- | 错误。H2A为强酸,电离方程式为H2A =2H+ +A2- | |
| D | BrCH2CH2CH2COOH +NaOH→BrCH2CH2CH2COONa +H2O | 正确 |