借你一个微笑
⑴李俊是个性格内向的学生,阅完的试卷一发下,我发现他眉头又锁到一起了,他只得了58分。
⑵一个从来不及格的学生,自信心有多差就不用说了。
⑶我合上教案面无表情地走出了教室,李俊跟了上来,他喉头动了一下,然后眼泪就要掉下来了。我站住,等他说话。同学们也围了上来,他的脸涨得通红。我静静地站着,希望他能开口,但他的嘴唇好像紧紧锁住了似的。
⑷他递过一张纸条:老师,我的物理太差,您能不能每天放学后为我补一个小时的课?
⑸我可以马上答应他,但面对这样的一个学生我决定“迂回”一下。我牵着他的手到僻静处说:“老师答应你的要求,可这两天我太忙,你等等好不好?”他有些失望,但还是点点头。我知道他中计了,接着说,你必须先借一样东西给我!他着急起来,可还是说不出一句话。
⑹“你每天借给我一个微笑,好不好?”
⑺这个要求太出乎他的意料,他很困惑地看着我。我耐心地等待着,他终于眼噙泪花艰难地咧开嘴笑了,尽管有些情不由衷。
⑻第二天上课,我注意到李俊抬头注视我,我微笑着,但他把脸避开了,显然他还不习惯对我回应。我让全班一起朗读例题,然后再让他重读一遍。他没有感觉我为难他,大大方方地站起来读了。也许想起了昨天对我的承诺,读完后,很困难地对我笑了笑。见他这样,我心生一计,又给他设置了一道障碍。我说,你复述一下题目的要求,这回他为难得快要哭了。不少同学对他的无能表现得很不耐烦,七嘴八舌地争着说起来,我制止住了大家。他终于张口了,语无伦次。我笑着让他坐下。
⑼他开始和同学来往了,一起上厕所,回教室……这样过了好长一段时间,我都没提为他补习的事。一天下课李俊又拦住我,我知道他要干什么,很幽默地向他摊开手。他一愣,老师您要什么?我说,你写给我的条子呀。他笑了:我不写条子了,您给我补补课吧。我面带笑容:“功课你不必着急,到时我会主动找你的,但我向你借的你还没给够我。”
⑽“好的,我一定给足您。”等他高高兴兴又蹦又跳地走出好一段路后,我才像想起来什么似的把他叫回来,递给他一张纸条,那里有我为他准备的一道题。我告诉他,一天之内把它做出来,可以和同学讨论也可以独立完成。我知道,他宁可“独吞”,也决不会和同学讨论的。这正是性格内向学生的最大弱点。下午他说还没做出来,我有点不高兴,说晚自习你还没做好,我可要收回承诺了。自习时我见他站在一个男生边上,忸忸怩怩很不自然的样子,我得意地笑了。就这样我先后为他写了4张纸条,题目一次比一次难。后来,纸条一到手他就迫不及待地和同学们争论开来。
⑾期末考试李俊成绩尚可,科科及格--看来我为他补的都差不多了。新学期刚开学,李俊休学了,因为他爸遇车祸瘫痪了,而他自小就被妈妈遗弃了--这也是他忧郁的一个原因。我有些担心,一个连话都不大愿说的少年,能担负起养护父亲的责任吗?
⑿星期天,我和几位朋友到茶室聊天。刚坐下就被一群小孩子围上了,硬要为我们擦皮鞋。只有一个小孩没冲进来,在外面吆喝着:擦皮鞋!擦皮鞋!……离开茶室,我从那个小孩子面前走过时,发现那孩子竟是李俊!
⒀“老师,让我为您擦一次皮鞋吧。”他说,脸上没有腼腆也没有沮丧。我答应了,伸过鞋子让他很用心地擦着。他一边擦一边说,他虽然不缠人,生意也不错。顾客告诉他,他的笑容很好看。
⒁我说是吗?他又笑着告诉我,不久他还会复学的。他学会了笑,他的笑,让他挣半天钱也能养活他和爸爸了。
⒂我也高兴起来,我说我一定等你回来。可转过身,我的泪水就出来了。李俊大声地在后面喊,老师您要笑呀,您不要哭!我点点头,反而呜咽有声了。
⒃我终于没有给他补课,是他为我补了一堂人生课。
1.通读这篇小说,简述题目“借你一个微笑”的深层含义。
_______________________________________________________________________________
______________________________________________________________________________
2.这篇小说的神态描绘逼真传神,第③自然段中画线语句写出了李俊什么样的心理?请简要回答。
____________________________________________________________________________
____________________________________________________________________________
3.第⑦自然段写李俊听说“我”要向他每天借一个微笑后,始而“很困惑地看着我”,终而“眼噙泪花艰难地咧开嘴笑了,尽管有些情不由衷”。由于受叙事方式的限制,作者没有写李俊复杂的心理活动,假如你是当时的李俊,请将你的心理活动描写出来。 (不少于25字)
______________________________________________________________________________
_____________________________________________________________________________
4.在这篇小说中,为了让李俊每天能够借给“我”一个微笑,作为老师的“我”具体做了哪几件事?请概括作答。
______________________________________________________________________________
______________________________________________________________________________
5.作者在第⑩自然段写道:“期末考试李俊成绩尚可,科科及格--看来我为他补的都差不多了”,而在小说结尾却又说“我终于没有给他补课”,这是否矛盾?为什么?请简要作答。
______________________________________________________________________________
_______________________________________________________________________________
6.在小说结尾,作者饱含深情地写道:“是他(李俊)为我补了一堂人生课”,请简要说说李俊为“我”补的这堂人生课的主要内容。
______________________________________________________________________________
______________________________________________________________________________
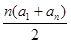 =
=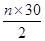 =210. n=14.∴选B.
=210. n=14.∴选B.