设X～B(1，9)，Y～E(λ)，且X，Y相互独立.证明Z=X+Y是连续型随机变量，

问题问答题

设X～B(1，9)，Y～E(λ)，且X，Y相互独立.

证明Z=X+Y是连续型随机变量，并求其概率密度.

答案

参考答案：

X	0	1
P	1-p	p

(0＜p＜1).

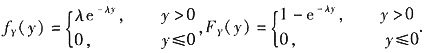
对任意实数z，Z的分布函数为
F_Z(z)=P(Z≤z)=P(X+Y≤z)=P(“X+Y≤z”∩Ω)
=P(“X+Y≤z”∩[“X=0”∪“X=1”])
=P(X+Y≤z，X=0)+P(X+Y≤z，X=1)
=P(Y≤z，X=0)+P(Y≤z-1，X=1)
=P(Y≤z)P(X=0)+P(Y≤z-1)P(X=1)
=(1-p)F_Y(z)+pF_Y(z-1).
由Y为连续型随机变量知Z=X+Y也是连续型随机变量，且

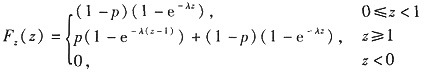
其概率密度为