问题
计算题
如图所示，竖直放置的光滑半圆形轨道与动摩擦因数为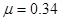
的水平面AB相切于B点，A、B两点相距L=2.5m，半圆形轨道的最高点为C，现将一质量为m=0.1kg的小球（可视为质点）以初速度v0=9m/s沿AB轨道弹出，g=10m/s2。求
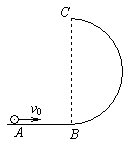
（1）小球到达B点时的速度大小及小球在A、B之间的运动时间；
（2）欲使小球能从最高点C水平抛出，则半圆形轨道的半径应满足怎样的设计要求？
（3）在满足上面（2）设计要求的前提下，半圆形轨道的半径为多大时可以让小球落到水平轨道上时离B点最远？最远距离是多少？
答案
（1）8 m/s 
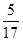s （2）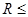
1.28m（3）R=0.8m，最远距离3.2m
（原创，考查平抛运动、牛顿第二定律、匀变速直线运动公式、动能定理，参考分值15分）
（1）小球从A到B，加速度大小为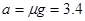
m/s2 （1分）
由运动学公式得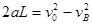
（1分）
解得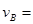
8 m/s（1分）
在A、B之间的运动时间 
s（1分）
（2）若小球恰能到达C点，由牛顿第二定律得mg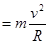 
（1分）
小球从B到C，由动能定理得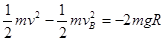 
（2分）
解得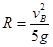
=1.28m（1分）
所以，欲使小球能从C点水平抛出，则半圆形轨道的半径应 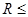1.28m（1分）
（3）小球从C点做平抛运动，由平抛运动的规律得2R =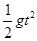
，x=vt（2分）
由（2）的求解知
解得x=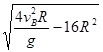
（1分）
当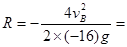
0.8m（<1.28m，能够到达C点）时水平射程最远（2分）
最远距离为xm=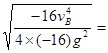
3.2m（1分）