问题
填空题
设矩阵A,B满足A*BA=2BA-8E,其中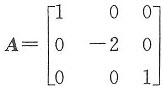 ,E为单位矩阵,A*为A的伴随矩阵,则B=()。
,E为单位矩阵,A*为A的伴随矩阵,则B=()。
答案
参考答案:
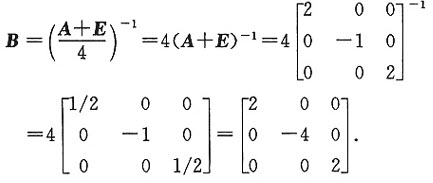
解析:
为消掉方程中未知矩阵A*,需在方程两边左乘A,然后右乘A-1以化简方程.
在所给方程的两边左乘A,则
AA*BA=2ABA-8A,即-2BA=2ABA-8A
在此方程两边右乘A-1,则
-2B=2AB-8E
即AB+B=4E,(A+E)B=4E
故

设矩阵A,B满足A*BA=2BA-8E,其中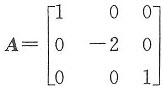 ,E为单位矩阵,A*为A的伴随矩阵,则B=()。
,E为单位矩阵,A*为A的伴随矩阵,则B=()。
参考答案:
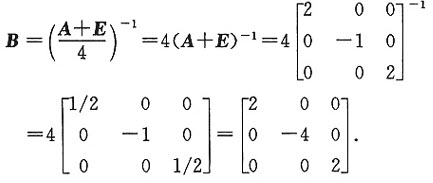
解析:
为消掉方程中未知矩阵A*,需在方程两边左乘A,然后右乘A-1以化简方程.
在所给方程的两边左乘A,则
AA*BA=2ABA-8A,即-2BA=2ABA-8A
在此方程两边右乘A-1,则
-2B=2AB-8E
即AB+B=4E,(A+E)B=4E
故
