问题
问答题
设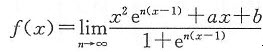 可导,试求a,b。
可导,试求a,b。
答案
参考答案:
因
en(x-1)=(ex-1)n,可视为F(x)g(n)(n→∞)型函数.这种类型函数常由|F(x)|=e|x-1|=1的解x=1作为x取值区间的分界点,分x>1,x=1,x<1三种情况求出极限.
求出极限后再根据连续和可导的必要条件列出a与b所满足的方程,联立解之即得a与b的值.
易求得
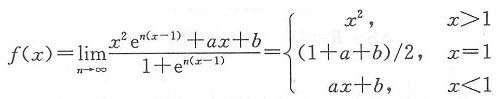
由f(x)可导知,f(x)在x=1处连续,于是有
f(1-0)=f(1+0)=f(1).
而
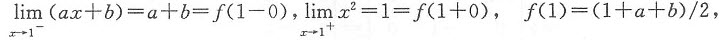
故
a+b=1=(1+a+b)/2.
又f(x)在x=1处可导,故
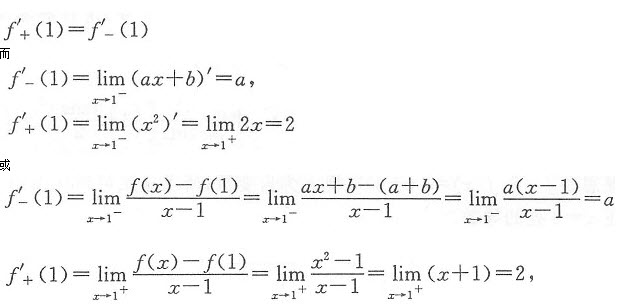 故a=2,从而b=1-a=1-2=-1.
故a=2,从而b=1-a=1-2=-1.
