问题
单项选择题
设函数z=f(x，y)满足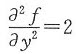
，且
f(x，0)=1，f’y(x，0)=x，
则f(x，y)=（）。
A．1-xy+y2
B．1+xy+y2
C．1-x2y+y2
D．1+x2y+y2
答案
参考答案：B
解析：
先在方程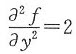
两边对y积分，再利用f’y(x，0)=x及f(x，0)=0确定相应常数.
在方程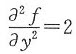两边对y积分得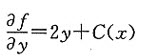
由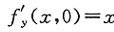
知
C(x)=x,即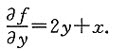
再积分得f(x,y)=y2+xy+C1(x)
再由f(x,0)=1知C1(x)=1. 于是
f(x,y)=1+xy+y2
仅(B)入选