(Ⅰ)因为△ABM是边长为的正三角形
所以圆M的半径r=,M到y轴的距离为d=r=,即椭圆的半焦距c=d=
此时点M的坐标为(,)…(2分)
因为点M在椭圆D:+=1(a>b>0)上
所以+=1
又a2-b2=c2=2
解得:a2=6,b2=4
所求椭圆D的方程为+=1…(4分)
(Ⅱ)由题意可知直线l的斜率存在,设直线斜率为k
直线l的方程为y=k(x+1),则有Q(0,k)
设P(x1,y1),由于P、Q、F三点共线,且=2
根据题意得(x1,y1-k)=2(-x1-1,-y1),解得…(6分)
又P在椭圆D上,故+=1
解得k=±
综上,直线l的斜率为k=±.…(8分)
(Ⅲ)由(Ⅰ)得:椭圆N的方程为+y2=1…①,
由于F1(1,0),设直线GK的方程为y=kx-2(k<0)…②,
则直线RS的方程为y=k(x-1)(k<0)…③
设H(x3,y3),K(x4,y4)
联立①②消元得:(1+2k2)x2-8kx+6=0,所以x3x4=
所以|GH|•|GK|=•=•=…(10分)
设R(x5,y5),S(x6,y6)
联立①③消元得:(1+2k2)x2-4k2x+2k2-2=0
所以x5+x6=,x5x6=y5y6=k2[x5x6-(x5+x6)+1]=3|RF1|•|F1S|=3•=3•=…(13分)
由=,化简得:k2+1=0,显然无解,
所以满足|GH|•|GK|=3|RF1|•|F1S|的直线GK不存在.…(14分)

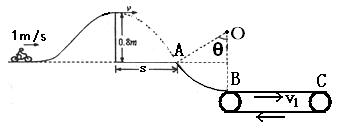
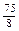 m,AB所对应的圆心角为θ=53o,人和车的总质量为180kg,特技表演的过程中到达传送带之前不计一切阻力(计算中取g=10m/s2,
m,AB所对应的圆心角为θ=53o,人和车的总质量为180kg,特技表演的过程中到达传送带之前不计一切阻力(计算中取g=10m/s2,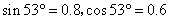 )。求:
)。求: