参考答案：

将增广矩阵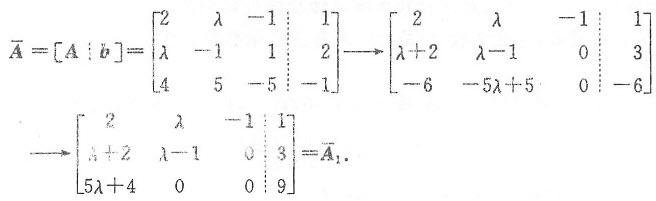化成能识别的秩与A的秩的大小的形式，然后对参数进行讨论，利用秩()与秩(A)的关系判别方程组解的情况．

对原方程组的增广矩阵施行初等行变换：

于是，当时，原方程组无解，因秩(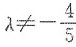)=3≠秩(A)=2．

当λ≠1且时，原方程组有唯一解，因秩()=秩(A)=3．

当λ=1时，原方程组有无穷多解，因秩()=秩(A)=2＜3．用初等行变换将进一步化成含有最高阶单位矩阵的矩阵：

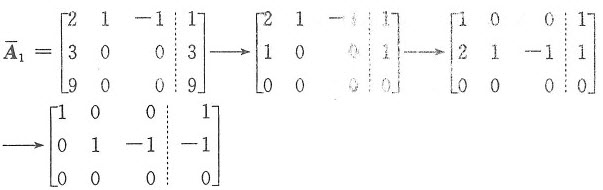
由特解及基础解系的简便求法得到其特解为

η=[1，-1，0]^T，

基础解系为

α=[0，1，1]^T，

因此，其通解为

x=kα+η，k为任意常数．