问题
填空题
方程x+y=ax2+by2+cx3(a+b≠0)确定了隐函数y=f(x),其中a,b,c均为常数,则在点(0,0)处曲线的曲率是()。
答案
参考答案:
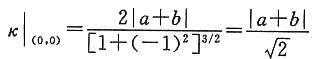
解析:
直接按曲线的曲率公式计算: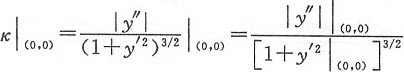
为此先要求出y’|(0,0),y"|(0,0).
在所给方程两边对x求导,得到
1+y’=2ax+2byy’+3cx2.
①
两边再对x求导,得到
y"=2a+2b(yy"+y’2)+6cx.
②
将x=0,y=0代入式①求得
y’|(0,0)=-1
再将x=0,y=0,y’=-1代入式②,得到
y"|(0,0)=2(a+b),
则所求曲率为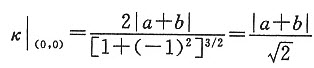 。
。
