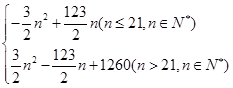问题
解答题
在等差数列{an}中，a16＋a17＋a18＝a9＝－36，其前n项和为Sn.
(1)求Sn的最小值，并求出Sn取最小值时n的值；
(2)求Tn＝|a1|＋|a2|＋…＋|an|.
答案
（1）当n＝20或21时，Sn取最小值且最小值为－630
（2）Tn＝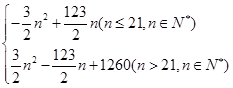
(1)设等差数列{an}的首项为a1，公差为d.
∵a16＋a17＋a18＝3a17＝－36，∴a17＝－12.
∴d＝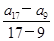
＝
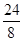＝3，
∴an＝a9＋(n－9)·d＝3n－63，an＋1＝3n－60.
令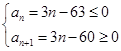
得20≤n≤21.
∴S20＝S21＝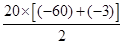
＝－630.
∴当n＝20或21时，Sn取最小值且最小值为－630.
(2)由(1)知前20项均小于零，第21项等于0.以后各项均为正数．
当n≤21时，
Tn＝－Sn＝－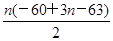
＝－
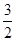n2＋
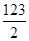n；
当n＞21时，Tn＝Sn－2S21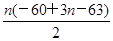＝－2S21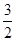＝n2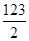－n＋1 260.
综上，Tn＝