问题
解答题
已知数列{an}的通项公式为an＝3n－1，在等差数列{bn}中，bn>0(n∈N*)，且b1＋b2＋b3＝15，又a1＋b1，a2＋b2，a3＋b3成等比数列．
(1)求数列{bn}的通项公式；
(2)求数列{an·bn}的前n项和Tn.
答案
（1）bn＝2n＋1（2）Tn＝n·3n.
(1)∵an＝3n－1(n∈N*)，∴a1＝1，a2＝3，a3＝9，在等差数列{bn}中，∵b1＋b2＋b3＝15，∴b2＝5，又a1＋b1，a2＋b2，a3＋b3成等比数列．
设等差数列{bn}的公差为d.
∴(1＋5－d)(9＋5＋d)＝64，解得d＝－10或d＝2，
∵bn>0(n∈N*)，∴舍去d＝－10，取d＝2，
∴b1＝3，∴bn＝2n＋1.
(2)由(1)知，Tn＝3×1＋5×3＋7×32＋…＋(2n－1)·3n－2＋(2n＋1)·3n－1，①
3Tn＝3×3＋5×32＋7×33＋…＋(2n－1)·3n－1＋(2n＋1)·3n，②
①－②得：－2Tn＝3×1＋2×3＋2×32＋…＋2×3n－1－(2n＋1)·3n＝3＋2(3＋32＋33＋…＋3n－1)－(2n＋1)·3n＝3＋2×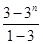
－(2n＋1)·3n＝3n－(2n＋1)·3n＝－2n·3n.∴Tn＝n·3n.