问题
解答题
已知an是一个等差数列，且a2=18，a14=—6．
（1）求an的通项an；
（2）求an的前n项和Sn的最大值并求出此时n值．
答案
（1）an=22-2n；（2）
时，
.
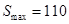题目分析：（1）利用等差数列通项公式求得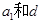
，写出通项；（2）求出
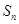，利用二次函数知识解答，注意数列中
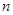取正整数.
试题解析：（1）由a1+d＝18,a1+13d＝−6解得：a1＝20，d＝−2，∴an=22-2n
（2）∵Sn＝na1+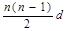
∴Sn＝n•20+
•(−2)，即 Sn=-n2+21n
∴Sn＝−(n−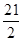
)2+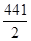
，∴n=10或11，有最大值S10（S11）=110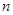项和.