问题
解答题
已知函数g(x)=ax2-4x+3的递增区间是(-∞，-2)。
（1）求a的值；
（2）设f(x)=g(x-2)，求f(x)在区间[-3，2]上的最大值和最小值。
答案
解：（1）因函数
的递增区间是(-∞，-2)，
则当a=0时，g(x)=-4x+3在R上单调递减与已知相矛盾，舍去；
当a≠0时，需a＜0且
，则a=-1；
所以a=-1。
（2）
，
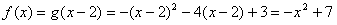则f(x)在[-3,0]上单调递增，在[0,2]上单调递减；
当x=0时，y有最大值7；
当x=-3时，y有最小值-2。