已知等差数列{an}满足:a2=5,a4+a6=22,数列{bn}满足b1+2b2+…
+2n-1bn=nan,设数列{bn}的前n项和为Sn.
(1)求数列{an},{bn}的通项公式;
(2)求满足13<Sn<14的n的集合.
(1)an=2n+1.bn=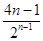 (n≥2).(2){n|n≥6,n∈N*}
(n≥2).(2){n|n≥6,n∈N*}
(1)设等差数列{an}的公差为d,则a1+d=5,(a1+3d)+(a1+5d)=22.
解得a1=3,d=2.∴an=2n+1.
在b1+2b2+…+2n-1bn=nan中,令n=1,则b1=a1=3,又b1+2b2+…+2nbn+1=(n+1)an+1,
∴2nbn+1=(n+1)an+1-nan.
∴2nbn+1=(n+1)(2n+3)-n(2n+1)=4n+3.
∴bn+1=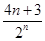 .∴bn=
.∴bn=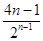 (n≥2).经检验,b1=3也符合上式,
(n≥2).经检验,b1=3也符合上式,
则数列{bn}的通项公式为bn=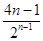 .
.
(2)Sn=3+7·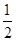 +…+(4n-1)·
+…+(4n-1)·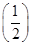 n-1,
n-1,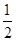 Sn=3·
Sn=3·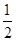 +7·
+7·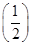 2+…+(4n-5)·
2+…+(4n-5)·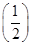 n-1+(4n-1)
n-1+(4n-1) 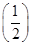 n.
n.
两式相减得
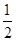 Sn=3+4
Sn=3+4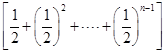 -(4n-1)·
-(4n-1)·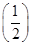 n,∴
n,∴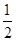 Sn=3+4·
Sn=3+4· -(4n-1)
-(4n-1) 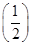 n.∴Sn=14-
n.∴Sn=14-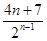 .
.
∴∀n∈N*,Sn<14.
∵数列{bn}的各项为正,∴Sn单调递增.又计算得S5=14-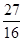 <13,S6=14-
<13,S6=14-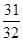 >13,
>13,
∴满足13<Sn<14的n的集合为{n|n≥6,n∈N*}
