问题
填空题
对于数列{an}，定义数列{an＋1－an}为数列{an}的“差数列”，若a1＝2，{an}的“差数列”的通项为2n，则数列{an}的前n项和Sn＝________.
答案
2n＋1－2
∵an＋1－an＝2n，
∴当n≥2时，
an＝(an－an－1)＋(an－1－an－2)＋…＋(a2－a1)＋a1＝2n－1＋2n－2＋…＋22＋2＋2＝
＋2＝2n.
当n＝1时，a1＝2也适合上式，
∴an＝2n(n∈N*)．
∴Sn＝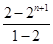
＝2n＋1－2.