问题
解答题
已知f(x)的定义域为(0,+∞),且满足f(4)=1,对任意x1,x2∈(0,+∞)都有f(x1?x2)=f(x1)+f(x2),当x∈(0,1)时,f(x)<0。
(1)求f(1);
(2)证明f(x)在(0,+∞)上是增函数;
(3)解不等式f(3x+1)+f(2x-6)≤3。
答案
解:(1)令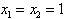 ,则f(1)=0;
,则f(1)=0;
(2)设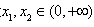 ,且
,且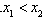 ,
,
则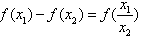 ,
,
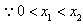 ,
,
∴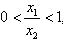 ,
,
又当x∈(0,1)时,f(x)<0,
∴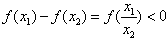 ,
,
∴f(x)在(0,+∞)上是增函数。
(3)令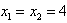 ,则
,则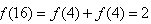 ;
;
令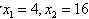 ,则
,则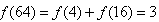 ,
,
∴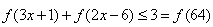 ,
,
可得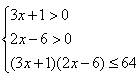 ,
,
解得: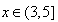 ,
,
∴不等式的解集为(3,5]。
