已知函数f(n)＝n2cos(nπ)，且an＝f(n)＋f(n＋1)，则a1＋a

问题选择题

已知函数f(n)＝n²cos(nπ)，且a_n＝f(n)＋f(n＋1)，则a₁＋a₂＋a₃＋…＋a₁₀₀＝(　　)

A．－100

B．0

C．100

D．200

答案

答案：A

若n为偶数，则a_n＝f(n)＋f(n＋1)＝n²－(n＋1)²＝－(2n＋1)，它是首项为a₂＝－5，公差为－4的等差数列；若n为奇数，则a_n＝f(n)＋f(n＋1)＝－n²＋(n＋1)²＝2n＋1，它是首项为a₁＝3，公差为4的等差数列．所以a₁＋a₂＋a₃＋…＋a₁₀₀＝(a₁＋a₃＋…＋a₉₉)＋(a₂＋a₄＋…＋a₁₀₀)＝50×3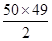＋×4＋50×(－5) 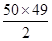×4＝－100，选A.