问题
解答题
某农村在2003年底共有人口1 500人，全年工农业生产总值为3 000万元，从2004年起计划10年内该村的总产值每年增加50万元，人口每年净增a人。设从2004年起的第x年年底(2004年为第一年，x∈N*)该村人均产值为y万元，
(Ⅰ)写出y与x之间的函数关系式；
(Ⅱ)为使该村的人均产值年年都有增长，那么该村每年人口的净增量不能超过多少人？
答案
解：(Ⅰ)由题意，得第x年总产值为3000+50x万元，人口数为1500+ax，
则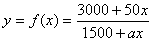
，x∈[1，10]，x∈N*．
(Ⅱ)由题意，得任取x1，x2∈[1，10]，x1＜x2，
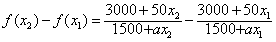
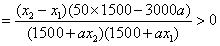恒成立，
则50×1500＞3000a，得a＜25，
因a为自然数，则该村每年人口的净增量不能超过24人．