问题
解答题
在平面直角坐标系xOy中,点E到两点F1(-1,0),F2(1,0)的距离之和为2
(1)写出C的方程; (2)设过点F2(1,0)的斜率为k(k≠0)的直线l与曲线C交于不同的两点M,N,点P在y轴上,且|PM|=|PN|,求点P纵坐标的取值范围. |
答案
(1)由椭圆的定义可知,点E的轨迹是以F1(-1,0),F2(1,0)为焦点,以2
为长轴的椭圆2
∵c=1,a=2
∴b=1
∴C的方程为
+y2=1x2 2
(2)由题意可得,直线MN的方程为y=k(x-1)
联立方程
可得,(1+2k2)x2-4k2x+2(k2-1)=0y=k(x-1)
+y2=1x2 2
设M(x1,y1),N(x2,y2),MN的中点E(x0,y0)
则x1+x2=
,y1+y2=k(x1+x2-2)=4k2 1+2k2 -2k 1+2k2
且△=16k4-8(1+2k2)(k2-1)>0
即1+k2>0
∵PM=PN且P在y轴上,设p (0,b)
∴x12+(y1-b)2=x22+(y2-b)2
整理可得,(x1-x2)(x1+x2)=(y2-y1)(y2+y1-2b)
∴x1+x2=k(y1+y2-2b)
代人可得,
=k(4k2 1+2k2
-2b)-2k 1+k2
∴b=-3k 1+2k2
∴2bk2+3k+b=0
∴△=9-8b2>0
∴-
<b<3 2 4
且b≠03 2 4

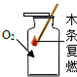 带火星的木条复燃
带火星的木条复燃 对着干燥玻璃片呼气
对着干燥玻璃片呼气 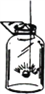 木炭在O2中燃烧
木炭在O2中燃烧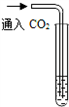 紫色石蕊溶液
紫色石蕊溶液