问题
解答题
函数f(x)对于任意实数x、y满足f(x+y)=f(x)+f(y)，且x＞0时，f(x)＜0，若f(1)=-1，求f(x)在[-4，4]上的最大值与最小值。
答案
解：令x=y=0，有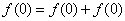
，
∴
，
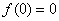令y=-x，有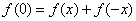
，
∴
，
∵
，
∴
，
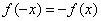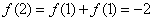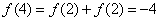故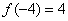
，
设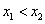
，则
，
∴
，
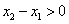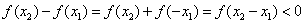因此，f(x)在[-4，4]上是减函数，
∴
。
搜题请搜索小程序“爱下问搜题”
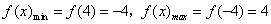函数f(x)对于任意实数x、y满足f(x+y)=f(x)+f(y)，且x＞0时，f(x)＜0，若f(1)=-1，求f(x)在[-4，4]上的最大值与最小值。
解：令x=y=0，有，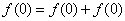
∴，
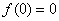令y=-x，有，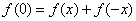
∴，
∵，
∴，
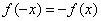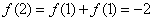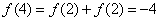故，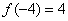
设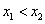，则，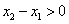
∴，
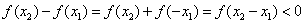因此，f(x)在[-4，4]上是减函数，
∴。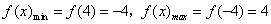