问题
填空题
已知函数f(x)=2x,等差数列{an}的公差为2,若f(a2+a4+a6+a8+a10)=4,则log2[f(a1)·f(a2)·f(a3)·…·f(a10)]="________."
答案
-6
因为数列{an}是公差为2的等差数列,
所以a2+a4+a6+a8+a10=5a2+40.
又因为f(a2+a4+a6+a8+a10)=4,
所以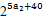 =4,即
=4,即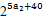 =22,
=22,
解得a2=- ,所以a1=-
,所以a1=-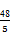 ,
,
因为f(a1)·f(a2)·f(a3)·…·f(a10)=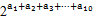 .
.
而a1+a2+a3+…+a10=10×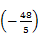 +
+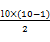 ×2=-6,
×2=-6,
所以log2[f(a1)·f(a2)·f(a3)·…·f(a10)]=log22-6=-6.
