问题
解答题
已知函数f(x)对任意实数x均有f(x)=kf(x+2),其中常数k为负数,且f(x)在区间[0,2]上有表达式f(x)=x(x-2)。
(I)求f(-1),f(2.5)的值;
(Ⅱ)写出f(x)在[-3,3]上的表达式,并讨论函数f(x)在[ -3,3]上的单调性;
(Ⅲ)求出f(x)在[-3,3]上的最小值与最大值,并求出相应的自变量的取值。
答案
解:(Ⅰ)f(-1)=kf(1)=-k
∵f(0.5)=kf(2.5)
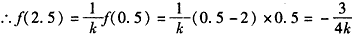 ;
;
(Ⅱ)∵对任意实数x,f(x)=kf(x+2)
∴f(x-2)=kf(x)
∴f(x)=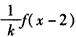
当-2≤x<0,0≤x+2<2,f(x)=kf(x+2)=kx(x+2);
当-3≤x<-2,-1≤x+2<0,f(x)=kf(x+2)=k2(x+2)(x+4);
当2≤x≤3时,0≤x-2≤1,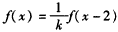
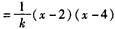 ;
;
故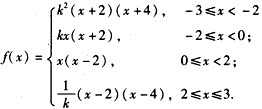
∴k<0
∴f(x)在[-3,-1]与[1,3]上为增函数,在[-1,1] 上为减函数;
(Ⅲ)由函数f(x)在[-3,3]上的单调性可知f(x)在x=-3或x=1处取得最小值f(-3)=-k2或f(1)=-1,而在x=-1或x=3处取得最大值,f(-1)=-k或f(3)=-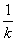
故有①k<-1时,f(x)在x=-3处取得最小值f(-3)=-k2,在x=-1处取得最大值,f(-1)=-k;
②k=-1时,f(x)在x=-3与x=l处取得最小值f(-3)= f(1)=-1,在x=-1与x=3处取得最大值f(-1)=f(3)=1
③-1<k<0时,f(x)在x=1处取得最小值f(1)=-1,在x=3处取得最大值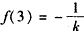 。
。
