问题
解答题
定义在[-2，2]上的偶函数g(x)满足：当x≥0时，g(x)单调递减；若g(1-m)＜g(m)，求m的取值范围。
答案
解：因为g(x)是[-2，2]上的偶函数，故g(x)= g(|x|)，
∴
，
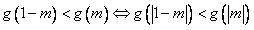又g(x)是[0，2]上的减函数，
∴原不等式等价于：
，
解得m的取值范围是：{m|-1≤m＜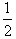
}。
搜题请搜索小程序“爱下问搜题”
定义在[-2，2]上的偶函数g(x)满足：当x≥0时，g(x)单调递减；若g(1-m)＜g(m)，求m的取值范围。
解：因为g(x)是[-2，2]上的偶函数，故g(x)= g(|x|)，
∴，
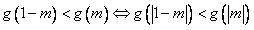又g(x)是[0，2]上的减函数，
∴原不等式等价于：，
解得m的取值范围是：{m|-1≤m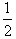＜}。