问题
解答题
已知函数f（x）=2x的定义域是[0，3]，设g（x）=f（2x）-f（x+2），
（1）求g（x）的解析式及定义域；
（2）求函数g（x）的最大值和最小值。
答案
解：（1）∵f（x）=2x，
∴g（x）=f（2x）-f（x+2）=22x-2x+2，
因为f（x）的定义域是[0，3]，
所以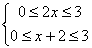
，解之得0≤x≤1，
于是g（x）的定义域为{x|0≤x≤1}。
（2）设g（x）=（2x）2-4×2x=（2x-2）2-4，
∵x∈[0，1]，
∴2x∈[1，2]，
∴当2x=2即x=1时，g（x）取得最小值-4；
当2x=1即x=0时，g（x）取得最大值-3。