问题
解答题
设函数f(x)的定义域是R,对于任意实数m,n,恒有f(m+n)=f(m)·f(n),且当x>0时,0<f(x)<1,
(1)求证:f(0)=1,且当x<0时,有f(x)>1;
(2)判断f(x)在R上的单调性。
答案
(1)证明:∵f(m+n)=f(m)f(n),
令m=1,n=0,则f(1)=f(1)f(0),
且由x>0时,0<f(x)<1,
所以f(0)=1;
设m=x=0,n=-x>0,
∴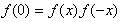 ,
,
∴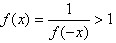 ;
;
(2)解: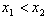 ,则
,则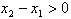 时,
时,
∴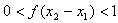 ,
,
∴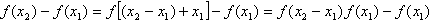
 ,
,
∴f(x)在R上单调递减。
