问题
解答题
已知函数f(x)=a·2x+b·3x,其中常数a,b满足ab≠0。
(1)若ab>0,判断函数f(x)的单调性;
(2)若ab<0,求f(x+1)>f(x)时x取值范围。
答案
解:(1)当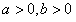 时,任意
时,任意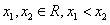 ,则
,则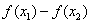 =
=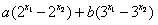
∵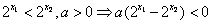 ,
,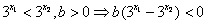
∴ ,函数f(x)在R上是增函数
,函数f(x)在R上是增函数
当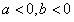 时,同理,函数f(x)在R上是减函数;
时,同理,函数f(x)在R上是减函数;
(2)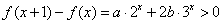
当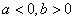 时,
时,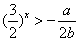 ,则
,则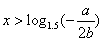
当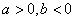 时,
时,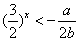 ,则
,则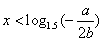 。
。
已知函数f(x)=a·2x+b·3x,其中常数a,b满足ab≠0。
(1)若ab>0,判断函数f(x)的单调性;
(2)若ab<0,求f(x+1)>f(x)时x取值范围。
解:(1)当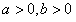 时,任意
时,任意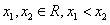 ,则
,则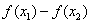 =
=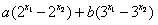
∵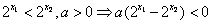 ,
,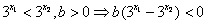
∴ ,函数f(x)在R上是增函数
,函数f(x)在R上是增函数
当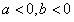 时,同理,函数f(x)在R上是减函数;
时,同理,函数f(x)在R上是减函数;
(2)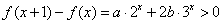
当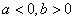 时,
时,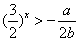 ,则
,则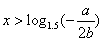
当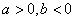 时,
时,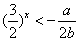 ,则
,则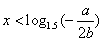 。
。