已知函数f(x)的图象在[a,b]上连续不断,定义:
f1(x)=min{f(t)|a≤t≤x}(x∈[a,b]),
f2(x)=max{f(t)|a≤t≤x}(x∈[a,b]),
其中,min{f(x)|x∈D}表示函数f(x)在D上的最小值,max{f(x)|x∈D}表示函数f(x)在D上的最大值。若存在最小正整数k,使得f2(x)-f1(x)≤k(x-a)对任意的x∈[a,b]成立,则称函数f(x)为[a,6]上的“k阶收缩函数”。 (Ⅰ)若f(x)=cosx,x∈[0,π],试写出f1(x),f2(x)的表达式;
(Ⅱ)已知函数f(x)=x2,x∈[-1,4],试判断f(x)是否为[-1,4]上的“k阶收缩函数”,如果是,求出对应的k;如果不是,请说明理由;
(Ⅲ)已知b>0,函数f(x)=-x3+3x2是[0,b]上的2阶收缩函数,求b的取值范围.
解:(Ⅰ)由题意可得:f1(x)=cosx,x∈[0,π],
f2(x)=1,x∈[0,π]。
(Ⅱ)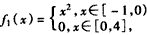 ,
,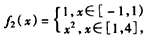 ,
,
 ,
,
当x∈[-1,0]时,1-x2≤k(x +1),∴k≥1-x,k>2;
当 x∈(0,1)时,1<k(x+1),∴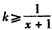 ,∴
,∴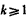 ;
;
当x∈[1,4]时,x2≤k(x+1) ∴k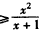 ,∴
,∴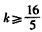 ,
,
综上所述,∴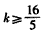 ,
,
即存在k=4,使得f(x)是[-1,4]的4阶收缩函数。
(Ⅲ)f′(x)=-3x2+6x=-3x(x-2),
令f′(x)=0得x=0或x=2,
函数f(x)的变化情如下:

令f(x)=0,解得x=0或3,
ⅰ)b≤2时,f(x)在[0,b]上单调递增,
因此,f2(x)=f(x)=-x3+3x2,f1(x)=f(0)=0,
因为f(x)=-x3+3x2是[0,b]上的2阶收缩函数,
所以,①f2(x)-f1(x)≤2(x-0)对x∈[0,b]恒成立;
②存在x∈[0,b],使得f2(x)-f1(x)>(x-0)成立,
①即:-x3+3x2≤2x对x∈[0,b]恒成立,由-x3+3x2≤2x,解得:0≤x≤1或x≥2,
要使-x3+3x2≤2x对x∈[0,b]恒成立,
需且只需0<b≤1;
②即:存在x∈[0,b],使得x(x2-3x+1)<0成立,
由x(x2-3x+1)<0得x<0或 ,
,
所以,需且只需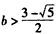 ,
,
综合①②可得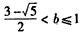 ;
;
ⅱ)2<b≤3时,f(x)在[0,2]上单调递增,在[2,b]上单调递减,
因此,f2(x)=f(2)=4,f1(x)=f(0)=0,
f2(x)-f1(x)=4,x-0=x,
显然当x=0时,f2(x)-f1(x)≤2(x- 0)不成立;
ⅲ)当b>3时,f(x)在[0,2]上单调递增,在[2,b]上单调递减,因此,f2(x)=f(2)=4,f1(x)=f(b)<0,
f2(x)-f1(x)=4-f(b)>4,x-0=x,
显然当x=0时,f2(x)-f1(x)≤2(x-0)不成立;
综合ⅰ)ⅱ)ⅲ)可得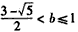 。
。
