问题
单项选择题
直线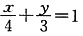 与椭圆
与椭圆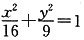 相交于A、B两点,该椭圆上点P,使得△PAB面积等于12,这样的点P共有()
相交于A、B两点,该椭圆上点P,使得△PAB面积等于12,这样的点P共有()
A.1个
B.2个
C.3个
D.4个
答案
参考答案:B
解析:
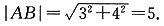 所以椭圆上点到直线的距离为
所以椭圆上点到直线的距离为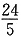 时恰有一个点P,小于
时恰有一个点P,小于 时,没有P,大于
时,没有P,大于 时,有2个点P,所以需求椭圆上的点到直线的最大距离,该点显然在与直线
时,有2个点P,所以需求椭圆上的点到直线的最大距离,该点显然在与直线
 平行且与椭圆相切的直线上,求得最远距离大于
平行且与椭圆相切的直线上,求得最远距离大于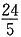 ,所以有2个点P.故选B.
,所以有2个点P.故选B.
直线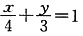 与椭圆
与椭圆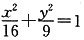 相交于A、B两点,该椭圆上点P,使得△PAB面积等于12,这样的点P共有()
相交于A、B两点,该椭圆上点P,使得△PAB面积等于12,这样的点P共有()
A.1个
B.2个
C.3个
D.4个
参考答案:B
解析:
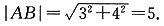 所以椭圆上点到直线的距离为
所以椭圆上点到直线的距离为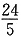 时恰有一个点P,小于
时恰有一个点P,小于 时,没有P,大于
时,没有P,大于 时,有2个点P,所以需求椭圆上的点到直线的最大距离,该点显然在与直线
时,有2个点P,所以需求椭圆上的点到直线的最大距离,该点显然在与直线
 平行且与椭圆相切的直线上,求得最远距离大于
平行且与椭圆相切的直线上,求得最远距离大于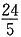 ,所以有2个点P.故选B.
,所以有2个点P.故选B.