问题
解答题
已知在递增等差数列{an}中，a1＝2，a1，a3，a7成等比数列，{bn}的前n项和为Sn，且Sn＝2n＋1－2.
(1)求数列{an}、{bn}的通项公式；
(2)设cn＝abn，求数列{cn}的前n项和Tn.
答案
（1）bn＝2n.（2）2n＋1－2＋n.
(1)∵a1，a3，a7成等比数列，∴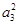
＝a1·a7，
设等差数列{an}的公差为d，则(2＋2d)2＝2(2＋6d)，d＞0，
∴d＝1，an＝n＋1.
又Sn＝2n＋1－2，b1＝S1＝2，当n≥2时，bn＝Sn－Sn－1＝2n＋1－2－2n＋2＝2n，经检验，n＝1适合此式，∴bn＝2n.
(2)∵cn＝abn＝2n＋1，
∴Tn＝(2＋1)＋(22＋1)＋…＋(2n＋1)＝(2＋22＋…＋2n)＋n＝2n＋1－2＋n.