问题
解答题
已知函数f（x）=log2（2x+1）。
（1）求证：函数f（x）在（-∞，+∞）内单调递增；
（2）记f-1（x）为函数f（x）的反函数、若关于x的方程f-1（x）=m+f（x）在[1，2]上有解，求m的取值范围。
答案
解：（1）任取
，则
∵
∴
∴
∴
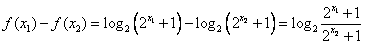
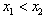
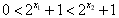
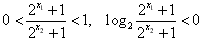
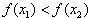，即函数f（x）在
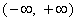内单调递增；
（2）
∴
=
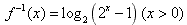
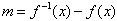
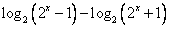
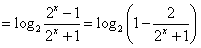
当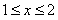
时，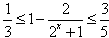
∴
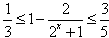
∴m的取值范围是
。
搜题请搜索小程序“爱下问搜题”
已知函数f（x）=log2（2x+1）。
（1）求证：函数f（x）在（-∞，+∞）内单调递增；
（2）记f-1（x）为函数f（x）的反函数、若关于x的方程f-1（x）=m+f（x）在[1，2]上有解，求m的取值范围。
解：（1）任取，则
∵
∴
∴
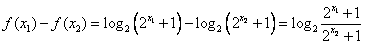
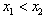
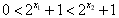
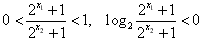
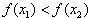∴，即函数f（x）在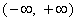内单调递增；
（2）
∴
=
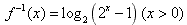
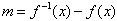
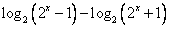
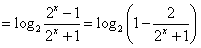
当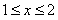时，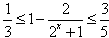
∴
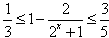
∴m的取值范围是。