问题
解答题
已知an＝n×0.8n(n∈N*)．
(1)判断数列{an}的单调性；
(2)是否存在最小正整数k，使得数列{an}中的任意一项均小于k？请说明理由．
答案
（1）a1，a2，a3，a4单调递增，a4＝a5，而a5，a6，…单调递减（2）k＝2
(1)∵an＋1－an＝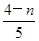
×0.8n(n∈N*)，∴n＜4时，an＜an＋1；n＝4时，a4＝a5；
n＞时，an＞an＋1.
即a1，a2，a3，a4单调递增，a4＝a5，而a5，a6，…单调递减．
(2)由(1)知，数列{an}的第4项与第5项相等且最大，最大项是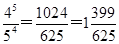
.
故存在最小的正整数k＝2，使得数列{an}中的任意一项均小于k.