已知数列{an}是等差数列，{bn}是等比数列，且a1＝b1＝2，b4＝54，a

问题解答题

已知数列{a_n}是等差数列，{b_n}是等比数列，且a₁＝b₁＝2，b₄＝54，a₁＋a₂＋a₃＝b₂＋b₃．

(1)求数列{a_n}和{b_n}的通项公式；

(2)数列{c_n}满足c_n＝a_nb_n，求数列{c_n}的前n项和S_n．

答案

（1）a_n＝6n－4 b_n＝2·3ⁿ^－1

（2）S_n＝7＋(6n－7)·3ⁿ

(1)设{a_n}的公差为d，{b_n}的公比为q，由b₄＝b₁q³，得q³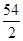＝＝27，从而q＝3，

因此b_n＝b₁·qⁿ^－1＝2·3ⁿ^－1，

又a₁＋a₂＋a₃＝3a₂＝b₂＋b₃＝6＋18＝24，∴a₂＝8，

从而d＝a₂－a₁＝6，故a_n＝a₁＋(n－1)·6＝6n－4．

(2)c_n＝a_nb_n＝4·(3n－2)·3ⁿ^－1，

令T_n＝1×3⁰＋4×3¹＋7×3²＋…＋(3n－5)·3ⁿ^－2＋(3n－2)·3ⁿ^－1．

3T_n＝1×3¹＋4×3²＋7×3³＋…＋(3n－5)·3ⁿ^－1＋(3n－2)·3ⁿ．

两式相减得

－2T_n＝1＋3×3¹＋3×3²＋3×3³＋…＋3×3ⁿ^－1－(3n－2)·3ⁿ＝1＋3×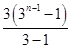－(3n－2)·3ⁿ＝1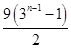＋－(3n－2)·3ⁿ，

∴T_n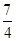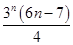＝＋，故S_n＝4T_n＝7＋(6n－7)·3ⁿ．